Diagram (category theory)

In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function from a fixed index set to the class of sets. A diagram is a collection of objects and morphisms, indexed by a fixed category; equivalently, a functor from a fixed index category to some category.

Diagrams are used in the definition of limit and colimits and the related notion of cones.

Contents 1 Definition 2 Examples 3 Cones and limits 4 Commutative diagrams 5 See also 5.1 Limits 5.2 Examples 6 References

Definition

Formally, a diagram of type J in a category C is a (covariant) functor

D : J → C

The category J is called the index category or the scheme of the diagram D. The actual objects and morphisms in J are largely irrelevant, only the way in which they are interrelated matters. The diagram D is thought of as indexing a collection of objects and morphisms in C patterned on J.

Although, technically, there is no difference between an individual diagram and a functor or between a scheme and a category, the change in terminology reflects a change in perspective, just as in the set theoretic case: one fixes the index category, and allows the functor (and, secondarily, the target category) to vary.

One is most often interested in the case where the scheme J is a small or even finite category. A diagram is said to be small or finite whenever J is.

A morphism of diagrams of type J in a category C is a natural transformation between functors. One can then interpret the category of diagrams of type J in C as the functor category C^J, and a diagram is then an object in this category.

Examples

• If J is a (small) discrete category, then a diagram of type J is essentially just an indexed family of objects in C (indexed by J).

• If J is a poset category then a diagram of type J is a family of objects D_i together with a unique morphism f_ij : D_i → D_j whenever i ≤ j. If J is directed then a diagram of type J is called a direct system of objects and morphisms. If the diagram is contravariant then it is called an inverse system.

• If 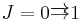, then a diagram of type J (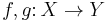) is called "two parallel morphisms": its limit is an equalizer, and its colimit is a coequalizer.

• If J = -1 ← 0 → +1, then a diagram of type J (A ← B → C) is a span, and its colimit is a pushout.

• If J = -1 → 0 ← +1, then a diagram of type J (A → B ← C) is a cospan, and its limit is a pullback.

Cones and limits

A cone of a diagram D : J → C is a morphism from the constant diagram Δ(N) to D. The constant diagram is the diagram which sends every object of J to an object N of C and every morphism to the identity morphism on N.

The limit of a diagram D is a universal cone to D. That is, a cone through which all other cones uniquely factor. If the limit exists in a category C for all diagrams of type J one obtains a functor

lim : C^J → C

which sends each diagram to its limit.

Dually, the colimit of diagram D is a universal cone from D. If the colimit exists for all diagrams of type J one has a functor

colim : C^J → C

which sends each diagram to its colimit.

Commutative diagrams

Diagrams and functor categories are often visualized by commutative diagrams, particularly if the index category is a finite poset category with few elements: one draws a commutative diagram with a node for every object in the index category, and an arrow for a generating set of morphisms, omitting identity maps and morphisms that can be expressed as compositions. The commutativity corresponds to the uniqueness of a map between two objects in a poset category. Conversely, every commutative diagram represents a diagram (a functor from a poset index category) in this way.

Not every diagram commutes, as not every index category is a poset category: most simply, the diagram of a single object with an endomorphism (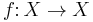), or with two parallel arrows (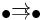; 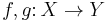) need not commute. Further, diagrams may be impossible (because infinite) or messy (because many objects or morphisms) to draw; however, schematic commutative diagrams (for subcategories of the index category, or with ellipses, such as for a directed system) are used to clarify such complex diagrams.

See also

• Commutative diagram
• Functor category

Limits

• Colimit
• Cone (category theory)
• Limit (category theory)

Examples

• Indexed family
• Direct system
• Inverse system
• Span
• Cospan

References

• Adámek, Jiří; Horst Herrlich, and George E. Strecker (1990). Abstract and Concrete Categories. John Wiley & Sons. ISBN 0-471-60922-6. http://katmat.math.uni-bremen.de/acc/acc.pdf.  Now available as free on-line edition (4.2MB PDF).